ph 求め方 公式で化学基礎の水素イオン濃度を計算

農業の現場で土壌分析や養液管理を行う際、pHの計算は避けて通れない重要なスキルです。なぜpHがずれるのか、その原因を化学的に理解するための公式と計算手順を徹底解説します。あなたは正確な値を把握できていますか？
農業情報
pH計算完全ガイド
⚗️
基礎公式の理解

対数（log）を用いた定義と基本式をマスター

🌱
農業への応用

土壌診断と肥料マネジメントへの活用法

⚠️
現場の落とし穴

活量係数や緩衝作用による測定誤差の正体

ph 求め方 公式

ph 求め方 公式
農業や園芸の現場において、土壌や養液の状態を数値化する「pH（水素イオン指数）」は、作物の生育を左右する最も基本的なパラメーターの一つです。しかし、単に測定器の数字を読み取るだけでなく、「なぜその値になるのか」「どのように計算されるのか」という化学的な背景を理解している指導者は多くありません。pHの定義である「ph 求め方 公式」を深く理解することは、異常値が出た際の原因究明や、精密な肥培管理を行う上で非常に強力な武器となります。本記事では、高校化学レベルの基礎から、現場で直面する「理論通りにいかないケース」までを網羅し、プロフェッショナルな視点で解説します。

 

ph 求め方 公式の基礎となる対数と定義

 

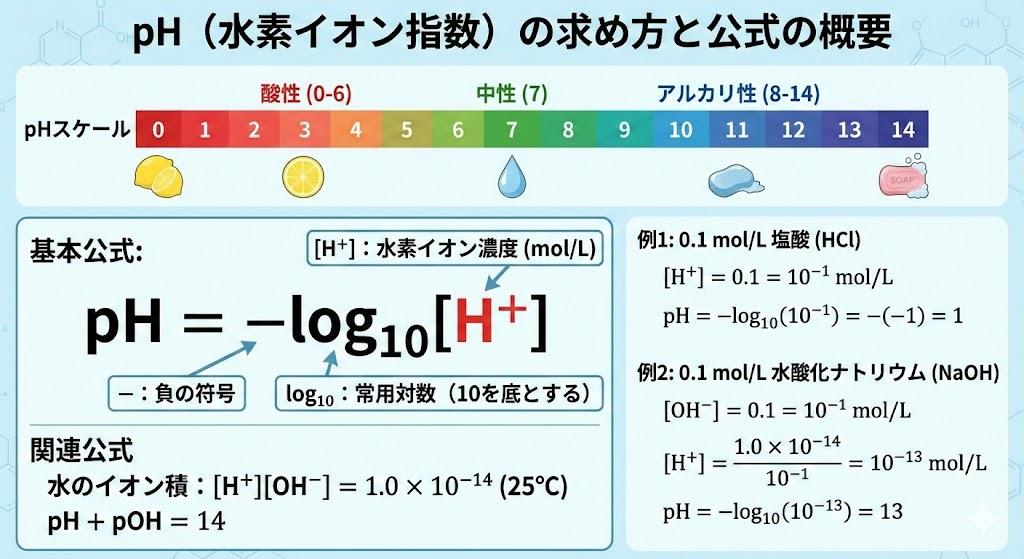
pH（Potential of Hydrogen）とは、水溶液中の水素イオン濃度 $H^+$ を対数を用いて表した指標です。この数値は、酸性・アルカリ性の度合いを直感的に扱いやすい $0$ から $14$ までの数字に変換するために考案されました。基本となる公式は以下の通り定義されています。

 

pH=−log⁡10H+pH = -\log_{10} H^+pH=−log10H+
この式において、$H^+$ は「水素イオン濃度（mol/L）」を表し、$\log_{10}$ は常用対数を意味します。つまり、pHとは「水素イオン濃度の逆数の常用対数」であると言い換えることができます 。

 

参考）【高校化学基礎】「水素イオン濃度とは」
​
農業現場でよくある「pHが1違うと酸性度はどれくらい違うのか？」という疑問に対し、この公式は明確な答えを持っています。対数スケールであるため、pHが $1$ 低下すると、水素イオン濃度は 10倍 になります。同様に、pHが $2$ 違えば濃度は 100倍 異なります。例えば、pH $6.0$ の土壌と pH $4.0$ の土壌では、酸の強さに100倍もの開きがあることになります。この感覚を数値として掴むことが、石灰資材の投入量を決定する際の重要な判断基準となります 。

 

参考）【高校理論化学】水素イオン濃度とpHの求め方！logの計算を…
​
計算のプロセスを具体化するために、いくつかのパターンを見てみましょう。

 

  • ケース1： 水素イオン濃度が $1.0 \times 10^{-2}$ mol/L の場合
    • 数式：$pH = -\log_{10} (1.0 \times 10^{-2}) = -(-2) = 2$
  • ケース2： 水素イオン濃度が $1.0 \times 10^{-7}$ mol/L の場合（中性）
    • 数式：$pH = -\log_{10} (1.0 \times 10^{-7}) = -(-7) = 7$

    このように、指数の部分（$10^{-n}$ の $n$）がそのままpHの値になるのが基本形です。しかし、現場では必ずしも綺麗な整数になるとは限りません。例えば濃度が $2.0 \times 10^{-3}$ mol/L のような場合、$\log_{10} 2 \approx 0.3$ という近似値を用いて計算する必要があります。

     

    pH=−log⁡10(2.0×10−3)=−(log⁡102+log⁡1010−3)=−(0.3−3)=2.7pH = -\log_{10} (2.0 \times 10^{-3}) = -(\log_{10} 2 + \log_{10} 10^{-3}) = -(0.3 - 3) = 2.7pH=−log10(2.0×10−3)=−(log102+log1010−3)=−(0.3−3)=2.7
    このように、簡単な対数の値を記憶しておくことで、電卓がない圃場でも概算が可能になります 。

     

    参考リンク：【pH計算】定義から公式、求め方、希釈や混合が絡む問題などを詳細に解説（受験のミカタ）

    ph 求め方 公式で重要な電離度とモル濃度

    pHを正確に求めるためには、単に酸の濃度を知るだけでは不十分です。「その酸がどれくらいイオンに分かれているか」を示す 電離度（$\alpha$） という概念を計算式に組み込む必要があります。特に有機酸肥料や土壌中の腐植酸など、農業に関わる多くの酸は「弱酸」に分類されるため、この電離度の理解が不可欠です。

     

    水素イオン濃度 $H^+$ を求めるための拡張された公式は以下のようになります。

     

    H+=c×α×nH^+ = c \times \alpha \times nH+=c×α×n
    ここで使用される変数の意味は以下の通りです。


    • $c$：モル濃度（mol/L） - 溶かした酸の濃度
    • $\alpha$：電離度（0 < $\alpha$ ≤ 1） - 溶けた酸のうち、実際にイオン化した割合
    • $n$：価数 - 酸1分子から放出される水素イオンの数（例：塩酸は1価、硫酸は2価）

    強酸と弱酸の違い
    塩酸（HCl）や硝酸（HNO$_3$）などの「強酸」は、水中でほぼ100%電離するため、電離度 $\alpha \approx 1$ とみなして計算します。

    一方、酢酸（CH$_3$COOH）やリン酸（H$_3$PO$_4$）などの「弱酸」は、水に溶けてもごく一部しか電離しません。例えば、0.1 mol/L の酢酸の電離度は約 0.016 程度です。

     

    この違いは、養液栽培でのpH調整剤の選定に大きく影響します。同じモル濃度の酸を投入しても、強酸を使うか弱酸を使うかで、pHの下がり方には劇的な差が生まれるのです 。

     

    参考）6-2. 水素イオン濃度とpH｜おのれー
    ​
    水のイオン積（$K_w$）との関係
    また、アルカリ性の溶液（石灰水など）のpHを求める場合は、一度水酸化物イオン濃度 $OH^-$ を求めてから、水のイオン積 $K_w$ を利用して変換する手順を踏みます。

     

    H+OH−=1.0×10−14(25∘Cにおいて)H^+OH^- = 1.0 \times 10^{-14} \quad (25^\circ \text{Cにおいて})H+OH−=1.0×10−14(25∘Cにおいて)
    pH+pOH=14pH + pOH = 14pH+pOH=14
    この関係式を知っていれば、「水酸化物イオン濃度がわかれば、14からpOHを引くことでpHが求まる」というショートカットが可能になります。例えば、$OH^- = 10^{-3}$ の場合、$pOH = 3$ となり、$pH = 14 - 3 = 11$ と計算できます 。

    参考）【高校化学】「水のイオン積とpH」(練習編)
    ​
    参考リンク：高校化学基礎 5分でわかる！水素イオン濃度と電離度の関係（Try IT）

    ph 求め方 公式を使った土壌診断と水素イオン濃度

    農業現場において「ph 求め方 公式」の知識が最も直接的に役立つのは、土壌診断とそれに基づく改良資材の計算です。土壌のpHは作物の根が養分を吸収する能力（可給性）に直結しており、不適切なpH管理は生理障害の主原因となります。

     

    適正pHと栄養素の溶解性
    一般的に多くの野菜は微酸性から中性（pH 6.0 ～ 6.5）を好みます。この範囲では、窒素（N）、リン酸（P）、カリウム（K）といった主要要素が最も効率よく吸収されます。

     

    • pHが低すぎる場合（酸性）： アルミニウムイオンが溶出し、根の生育を阻害します。また、リン酸がアルミニウムや鉄と結合して不可給態となり、欠乏症を引き起こします。
    • pHが高すぎる場合（アルカリ性）： 鉄、マンガン、亜鉛などの微量要素が溶けにくくなり、欠乏による葉の黄化（クロロシス）が発生します 。

      参考）土壌pHとは、野菜作りの基本の土作りと測定・調整方法
      ​

    アレニウス表と石灰所要量の計算
    土壌診断の結果、pHが目標値より低い場合、石灰質肥料を用いて矯正を行いますが、ここで単純な比例計算は通用しません。土壌にはpHの変化に抵抗する力（緩衝能）があるためです。

     

    正確な石灰施用量を求めるには、以下の要素を考慮する必要があります。

     

    1. 目標pHと現在pHの差
    2. 土壌の種類（土性）： 砂質土は緩衝能が低く、粘土質や腐植に富む土は緩衝能が高い。
    3. 腐植含量

    「アレニウス表」と呼ばれる対応表は、これらの要素を組み合わせて必要な炭酸カルシウムの量を算出するために使われます。例えば、pH 5.0 の土壌を pH 6.5 に矯正する場合、砂壌土なら少量の石灰で済みますが、黒ボク土のような腐植に富む土壌では、2倍～3倍の石灰を投入しないとpHは動きません。公式としての計算だけでなく、土壌の「物理性」という係数を掛け合わせる視点が、実践的な農業では求められます 。

     

    参考）https://www.zennoh.or.jp/members/pdf/gijyutu_1_01b.pdf
    ​
    作物別適正pHの例

    作物カテゴリ 好適pH範囲 特記事項
    ホウレンソウ 6.5 - 7.0 酸性に極めて弱い。低pHでは発芽不良や立枯れが発生。
    トマト・ナス 6.0 - 6.5 多くの果菜類の標準範囲。
    ジャガイモ 5.0 - 6.0 そうか病予防のため、やや酸性側で管理する。
    ブルーベリー 4.5 - 5.0 強酸性を好む。ピートモス等でpHを下げる調整が必要。

    参考リンク：土壌pHとは？野菜作りの基本となる土壌改良と石灰資材の計算方法（農家web）

    ph 求め方 公式と化学的な緩衝作用のメカニズム

    pHの計算を行う上で、計算値と実測値が合わない最大の要因の一つが「緩衝作用」です。緩衝作用とは、少量の酸や塩基を加えてもpHがほとんど変化しない現象のことを指します。これは農業、特に養液栽培や培地管理において極めて重要な化学的メカニズムです。

     

    緩衝液の公式：ヘンダーソン・ハッセルバルヒの式
    緩衝作用を理解するための計算式として、ヘンダーソン・ハッセルバルヒの式が知られています。弱酸とその塩（例：酢酸と酢酸ナトリウム）が混在する溶液のpHは以下のように表されます。

     

    pH=pKa+log⁡10A−HApH = pK_a + \log_{10} \frac{A^-}{HA}pH=pKa+log10HAA−


    • $pK_a$：酸解離定数の逆数の対数（その酸固有の強さ）
    • $HA$：酸のモル濃度
    • $A^-$：その塩（共役塩基）のモル濃度

    この式が示唆しているのは、「酸とその塩の比率が等しいとき（$\log 1 = 0$ のとき）、溶液のpHは $pK_a$ に等しくなり、その周辺で最も強い緩衝能力を発揮する」という事実です 。

     

    参考）Redirecting...
    ​
    農業における緩衝作用の実例

    1. リン酸緩衝液としての土壌

      土壌中にはリン酸塩が多く含まれており、これが天然の緩衝剤として働きます。リン酸二水素イオン（H$_2$PO$_4^-$）とリン酸水素イオン（HPO$_4^{2-}$）の平衡関係により、肥料として酸を投入しても急激なpH低下を防いでいます。これは植物にとって急激な環境変化を避ける安全装置として機能しますが、逆に言えば「pHを下げたいときに下がりにくい」原因ともなります。

       

    2. 重炭酸緩衝系（地下水・養液）

      灌漑水に含まれる重炭酸イオン（HCO$_3^-$）も強力な緩衝作用を持ちます。原水のpHが高く、かつ重炭酸濃度が高い場合、計算通りの酸を添加してもpHが下がらない現象（酸の中和消耗）が起こります。この場合、単純な $H^+$ の計算ではなく、中和滴定曲線を作成して酸の必要量を決定するプロセスが必要になります 。

       

      参考）https://nvlpubs.nist.gov/nistpubs/jres/65A/jresv65An3p267_A1b.pdf
      ​

    参考リンク：pH計算の実際と近似が成立する条件、緩衝作用の数式的理解（Chemist Eyes）

    ph 求め方 公式の定義に関わる活量係数の影響

    最後に、教科書的な「ph 求め方 公式」の盲点であり、かつ測定における最も専門的な領域である「活量（Activity）」について解説します。実は、厳密な化学的定義において、pHは水素イオン「濃度」ではなく、水素イオン「活量」の対数として定義されています。

     

    pH=−log⁡10aH+=−log⁡10(γ×H+)pH = -\log_{10} a_{H^+} = -\log_{10} (\gamma \times H^+)pH=−log10aH+=−log10(γ×H+)
    ここで登場する $a_{H^+}$ が水素イオン活量、そして $\gamma$（ガンマ）または $f$ が 活量係数 と呼ばれる補正値です。

    通常の高校化学や簡易的な計算では $\gamma = 1$（濃度と活量が等しい）と仮定して計算しますが、これは「非常に薄い水溶液」に限った話です 。

    参考）理論的なpHの定義 - HORIBA
    ​
    なぜ活量係数が重要なのか
    農業、特に高濃度の液肥を使用する養液栽培や、EC（電気伝導度）が高い塩類集積土壌においては、溶液中に多量のイオンが存在します。イオン同士は電気的な引力や反発力を及ぼし合うため、水素イオンが自由に動き回ることが制限されます。この「動きにくさ」を補正するのが活量係数です。

     

    イオン濃度が高くなる（溶液が濃くなる）と、活量係数 $\gamma$ は $1$ よりも小さくなります。

     

    つまり、実際の濃度 $H^+$ は高いのに、見かけ上の働き（活量）は低くなるため、計算よりもpHが高く測定されるという現象が起こります。

     

    例えば、硝酸やリン酸カリウムを高濃度で溶かした濃厚原液タンクのpHを測定する場合、単純な濃度計算から導き出される理論値と、ガラス電極法（活量を測定する方式）で得られる実測値にはズレが生じます。これは測定器の故障ではなく、熱力学的な必然です。「公式通りに計算したのに数値が合わない」と悩む技術者の多くが、この活量係数の罠に見落としがあります。

     

    精密な化学管理が求められる植物工場や研究レベルの栽培試験では、デバイ・ヒュッケルの式などを用いて活量係数を推定し、より厳密なpH管理を行うことが求められます 。

     

    参考）https://lab-brains.as-1.co.jp/for-biz/2021/08/36392/
    ​
    参考リンク：理論的なpHの定義と活量係数、ガラス電極法が測定している真の値（HORIBA）

     

    default_api:search_web{queries:ec とは 簡単に 農業 メリット デメリット,農業 EC 成功事例 初心者 始め方,ネットショップ 開設 農業 直販 比較,農業EC 独自視点 未来 トレンド 2025,農家 直販 法律 トラブル防止}

     

     


    pH試験紙 (pH0-14)